More pages: 1 2
3 4 5
Triangulation
Wednesday, January 14, 2009 | Permalink
When you look at a highly tessellated model it's generally understood that it will be vertex processing heavy. Not quite as widely understood is the fact that increasing polygon count also adds to the fragment shading cost, even if the number of pixels covered on the screen remains the same. This is because fragments are processed in quads. So whenever a polygon edge cuts through a 2x2 pixel area, that quad will be processed twice, once for both of the polygons covering it. If several polygons cut through it, it may be processed multiple times. If the fragment shader is complex, it could easily become the bottleneck instead of the vertex shader. The rasterizer may also not be able to rasterize very thin triangles very efficiently. Since only pixels that have their pixel centers covered (or any of the sample locations in case of multisampling) are shaded the quads that need processing may not be adjacent. This will in general cause the rasterizer to require additional cycles. Some rasterizers may also rasterize at fixed patterns, for instance an 4x4 square for a 16 pipe card, which further reduces the performance of thin triangles. In addition you also get overhead because of less optimal memory accesses than if everything would be fully covered and written to at once. Adding multisampling into the mix further adds to the cost of polygon edges.
The other day I was looking at a particularly problematic scene. I noticed that a rounded object in the scene was triangulated pretty much as a fan, which created many long and thin triangles, which was hardly optimal for rasterization. While this wasn't the main problem of the scene it made me think of how bad such a topology could be. So I created a small test case to measure the performance of three different layouts of a circle. I used a non-trivial (but not extreme) fragment shader.
The most intuitive way to triangulate a circle would be to create a fan from the center. It's also a very bad way to do it. Another less intuitive but also very bad way to do it is to create a triangle strip. A good way to triangulate it is to start off with an equilateral triangle in the center and then recursively add new triangles along the edge. I don't know if this scheme has a particular name, but I call it "max area" here as it's a greedy algorithm that in every step adds the triangle that would grab the largest possible area out of the remaining parts on the circle. Intuitively I'd consider this close to optimal in general, but I'm sure there are examples where you could beat such a strategy with another division scheme. In any case, the three contenders look like this:
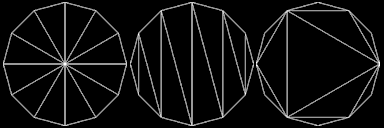
And their performance look like this. The number along the x-axis is the vertex count around the circle and the y-axis is frames per second.
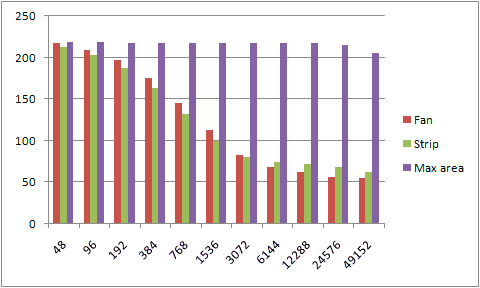
Adding multisampling into the mix further adds to the burden with the first two methods, while the max area division is still mostly unaffected by the added polygons all the way across the chart.

Seth
Saturday, January 17, 2009
Rohit Garg,
Triangle fans are already gone in D3D10 and deprecated in OpenGL3. One thing you could do to simulate them, though, is to use an index array to connect the vertices in a similar way.
Seth
Saturday, January 17, 2009
On second thought, they might not be deprecated in OpenGL3. From the specification:
Deprecated: Quadrilateral and polygon primitives - vertex array drawing modes
POLYGON, QUADS, and QUAD_STRIP (section 2.6.1, related descriptions of
rasterization of non-triangle polygons in section 3.6, and all associated state.
Rohit Garg
Saturday, January 17, 2009
Simon,
I meant an object like a cone, for which the natural tesselation seems to be a triangle fan. I wonder why triangle fans have been thrown out in new APIs? Are they inefficient like immediate mode rendering or what?
Humus
Saturday, January 17, 2009
Rohit Garg,
I don't know what was the exact motivation for removing it in DX10, but it should be noted that fans have very limited utility. Back when people called glVertex3f() and vertex buffers didn't exist and everything was very low-poly anyway I suppose it was nice for some things. Personally the only times I've used it is for things like fullscreen quads, which is equally well done with a triangle strip. I don't think fans are necessarily slower than other primitive types, or if it really takes that much chip area to support, but it just doesn't add any functionality that can't be done with other primitive types. I suppose it also doesn't fit very well with the adjacency stuff for the geometry shader.
LogicalError
Thursday, January 22, 2009
Why did you make a fan with an extra vertex from the center? wouldn't you be able to make a fan from one of the other vertices (would work with any convex polygon) instead? that would save one vertex and 2 triangles.. would be a more fair comparison i think
Humus
Friday, January 23, 2009
I used it as an intuitive way to render a circle. Yes, you could drop the center vertex; however, there's no advantage to that. Instead of creating thin triangles towards the center it creates thin triangles across the whole circle and hence performs comparable to strips.
Chris
Friday, January 23, 2009
Is there an algorithm that could take a mesh and optimize it to reduce edge lengths?
Humus
Saturday, January 24, 2009
Well, I don't know any standard algorithm with a name or anything, but you could simply for every edge look at the two triangles that are connected through that edge and see if it would make sense to replace it with an edge crossing the other way. You'd need some criteria other than shorter distance though for general meshes, for instance the two triangles would need to be reasonably coplanar and the two triangles would need to be convex quad for it to work. Then you'd need to repeat until no further reductions can be found. Without having tested this I suppose it would do a decent job on many meshes. However, there are clearly cases where it would help. For instance in the strip case here it would probably not be able to reduce it to something less. You'd need to consider larger areas in each step to be able to find a better triangulation.
More pages: 1 2
3 4 5





